Topological invariants

Calculation of Berry phase and Chern number for a magneto-optical photonic crystal.

import time

import matplotlib.pyplot as plt

import protis as pt

pt.set_backend("autograd")
# pt.set_backend("torch")
bk = pt.backend


pi = bk.pi
plt.ion()
plt.close("all")

Reference results are taken from [blancodepaz2020].

a = 1
lattice = pt.Lattice([[a, 0], [0, a]], discretization=2**9)

Define the permittivity

rod = lattice.circle(center=(0.5, 0.5), radius=0.11)
epsilon = lattice.ones()
epsilon[rod] = 15
mu = lattice.ones()
one = lattice.ones()
zero = lattice.zeros()
mu = pt.block_z_anisotropic(one, zero, zero, one, one)
mu[0, 0, rod] = mu[1, 1, rod] = 14
mu[0, 1, rod] = 12.4j
mu[1, 0, rod] = -12.4j

We define here the wavevector path:

Gamma = (0, 0)
X = (pi / a, 0)
M = (pi / a, pi / a)
sym_points = [Gamma, X, M, Gamma]

Nb = 31
kpath = pt.init_bands(sym_points, Nb)

Calculate the band diagram:

polarization = "TM"
nh = 200


def compute_bands(epsilon, mu):
    sim = pt.Simulation(lattice, epsilon=epsilon, mu=mu, nh=nh)
    ev_band = []
    for kx, ky in kpath:
        sim.k = kx, ky
        sim.solve(polarization, vectors=False)
        ev_norma = sim.eigenvalues * a / (2 * pi)
        ev_band.append(ev_norma.real)
    return ev_band


ev_band0 = compute_bands(epsilon, mu=1)


ev_band = compute_bands(epsilon, mu)

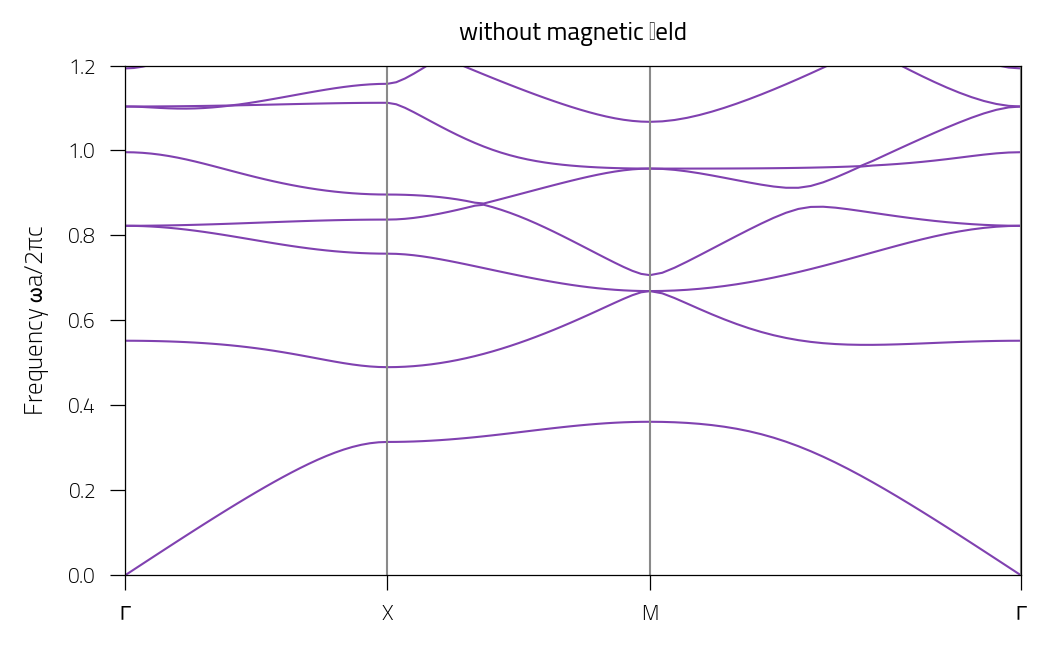
Plot the bands (without magnetic field):

labels = ["$\Gamma$", "$X$", "$M$", "$\Gamma$"]


plt.figure()
pt.plot_bands(sym_points, Nb, ev_band0, color="#8041b0", xtickslabels=labels)
plt.ylim(0, 1.2)
plt.ylabel(r"Frequency $\omega a/2\pi c$")
plt.title("without magnetic field")
plt.tight_layout()

/builds/protis/protis.gitlab.io/protis/examples/plot_chern.py:99: UserWarning: Glyph 64257 (\N{LATIN SMALL LIGATURE FI}) missing from current font.
  plt.tight_layout()

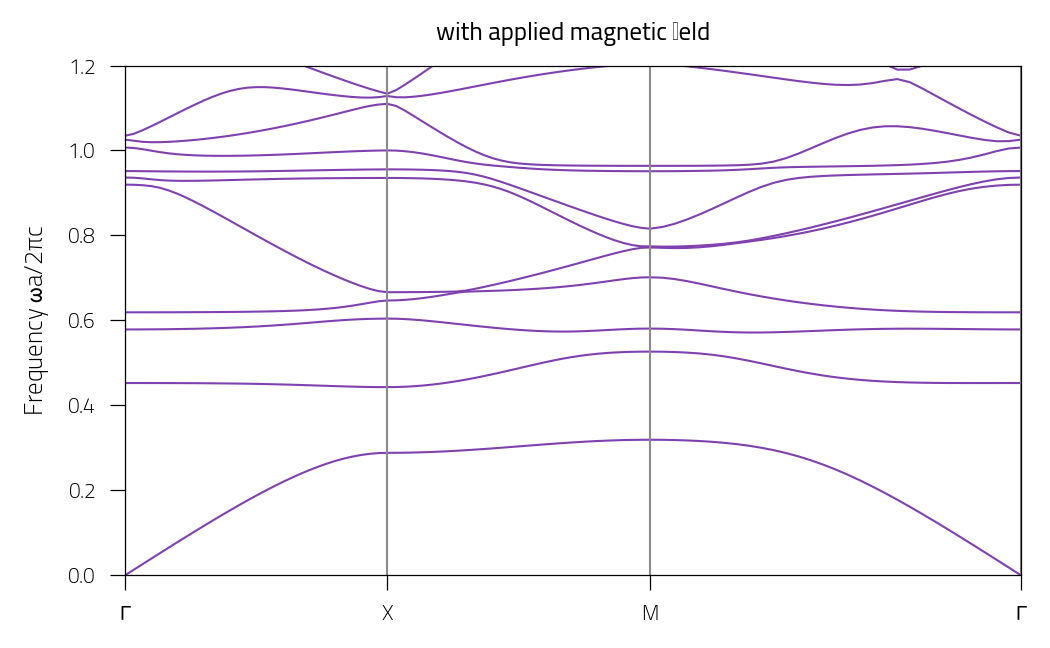
Plot the bands (with magnetic field):

plt.figure()
pt.plot_bands(sym_points, Nb, ev_band, color="#8041b0", xtickslabels=labels)
plt.ylim(0, 1.2)
plt.ylabel(r"Frequency $\omega a/2\pi c$")
plt.title("with applied magnetic field")
plt.tight_layout()

/builds/protis/protis.gitlab.io/protis/examples/plot_chern.py:109: UserWarning: Glyph 64257 (\N{LATIN SMALL LIGATURE FI}) missing from current font.
  plt.tight_layout()

Compute modes in the first Brillouin zone:

sim = pt.Simulation(lattice, epsilon=epsilon, mu=mu, nh=nh)


t = -time.time()

method = "fourier"

n_eig = 3
nk = 31
kx = ky = bk.linspace(0, 2 * pi / a, nk)
Kx, Ky = bk.meshgrid(kx, ky)


if method == "fourier":
    eigenmodes = bk.empty((nk, nk, sim.nh, n_eig), dtype=bk.complex128)
else:
    eigenmodes = bk.empty((nk, nk, *lattice.discretization, n_eig), dtype=bk.complex128)


for i in range(nk):
    _mode = []
    for j in range(nk):
        k = kx[i], ky[j]
        sim.k = k
        eigs, modes = sim.solve(polarization)
        if method == "fourier":
            eigenmodes[i, j] = modes[:, :n_eig]
        else:
            eigenmodes[i, j] = sim.get_modes(range(n_eig))

Compute Berry curvature and Chern number

for imode in range(n_eig):
    mode = (
        eigenmodes[:, :, :, imode]
        if method == "fourier"
        else eigenmodes[:, :, :, :, imode]
    )
    phi = sim.get_berry_curvature(kx, ky, mode, method=method)
    C = sim.get_chern_number(kx, ky, phi)
    print(f"Mode {imode+1}: Chern number = {C}")

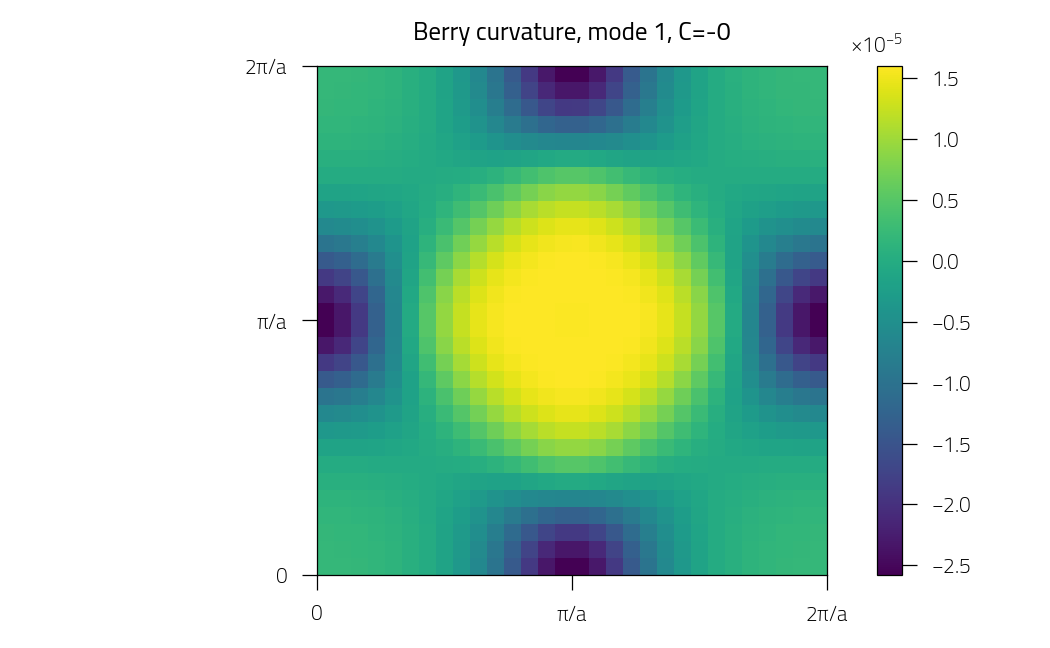
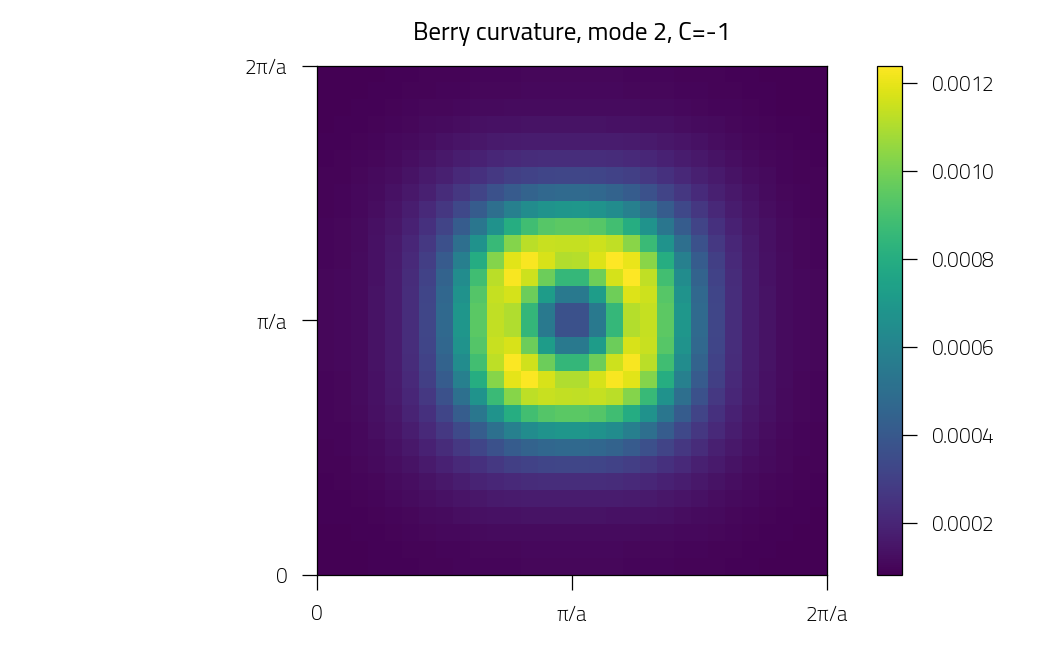
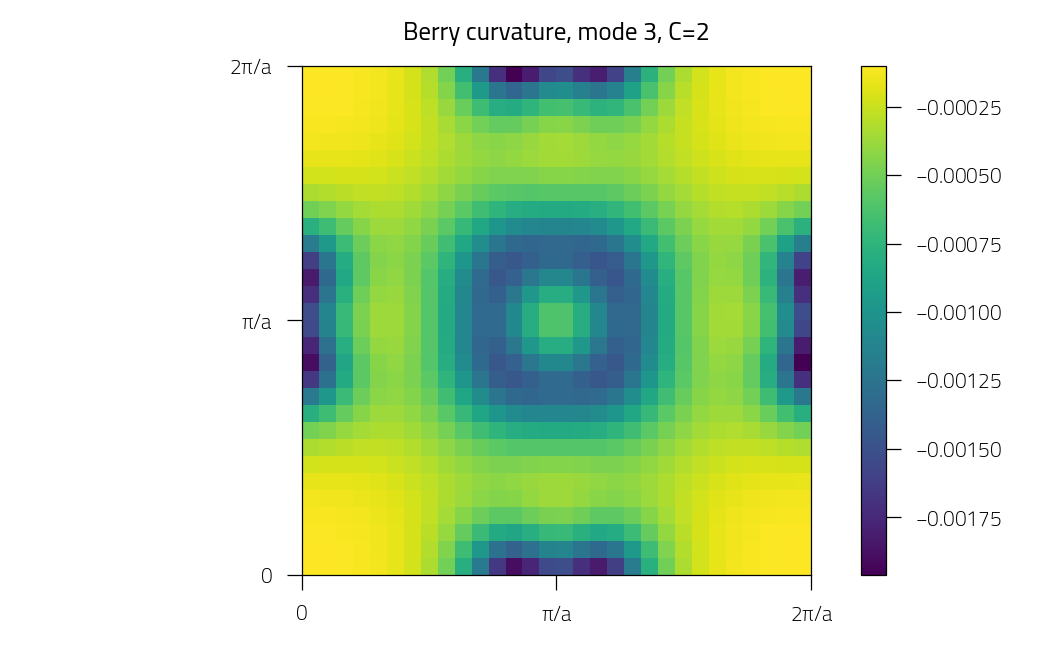
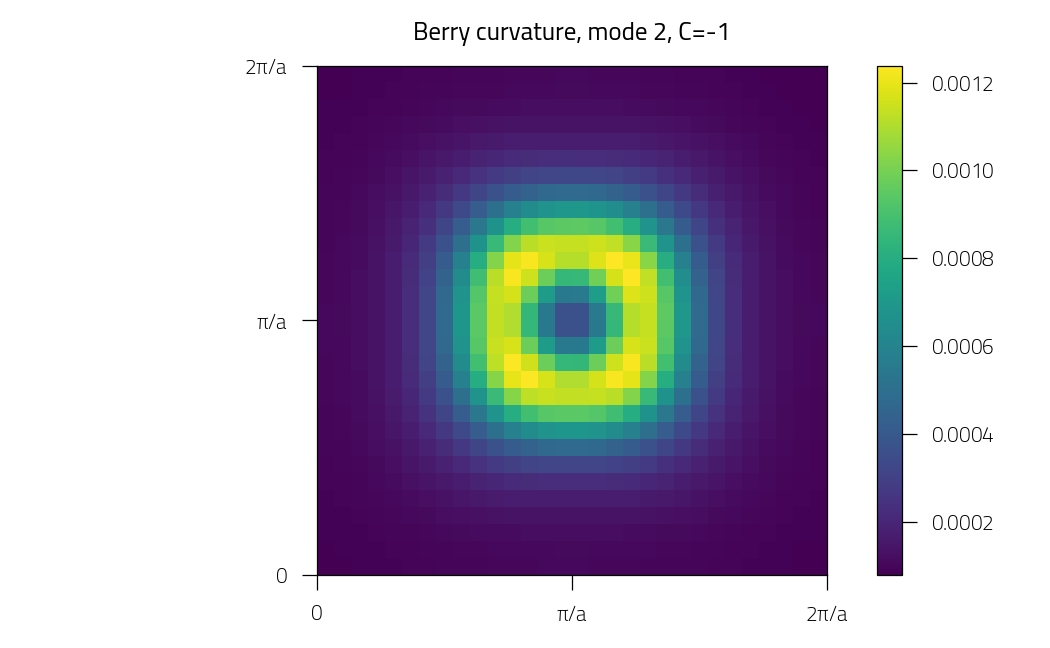
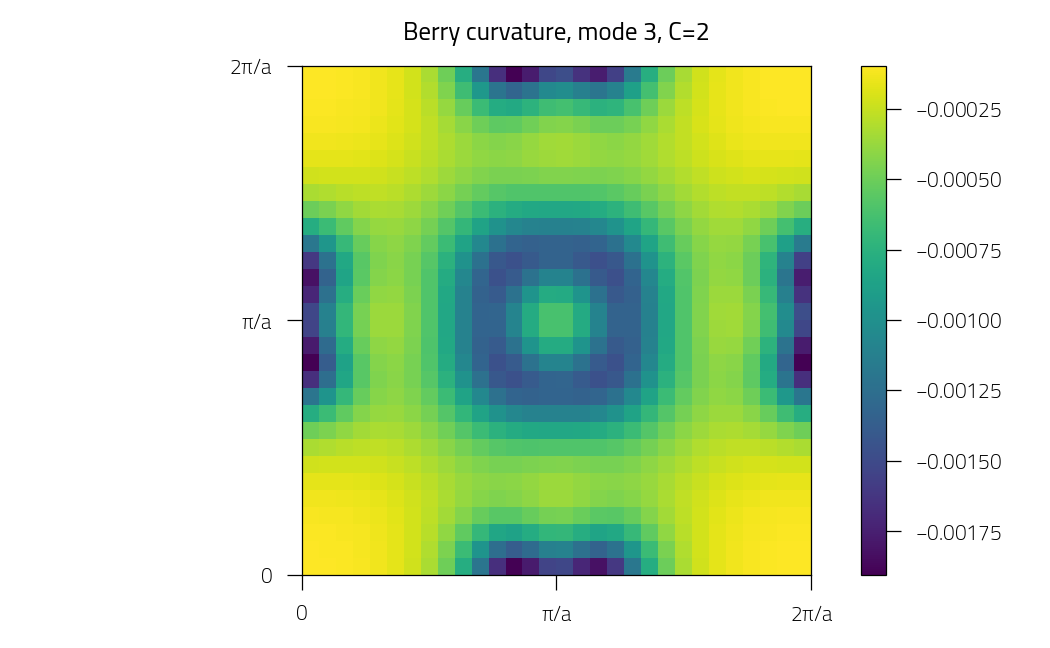
    plt.figure()
    plt.pcolormesh(kx, ky, phi)
    plt.axis("scaled")
    plt.xticks([0, pi / a, 2 * pi / a], ["0", r"$\pi/a$", r"$2\pi/a$"])
    plt.yticks([0, pi / a, 2 * pi / a], ["0", r"$\pi/a$", r"$2\pi/a$"])
    plt.title(f"Berry curvature, mode {imode+1}, C={C:.0f}")
    plt.colorbar()
    plt.tight_layout()
    plt.pause(0.001)


t += time.time()
print(f"Elapsed time: {t:.1f}s")

• 
• 
• 

Mode 1: Chern number = -0.00026902036635345996
Mode 2: Chern number = -0.9996736875242193
Mode 3: Chern number = 1.9738567117040693
Elapsed time: 67.0s

Same but with reduced Bloch mode expansion

t = -time.time()

U = (0, 2 * pi / a)
V = (2 * pi / a, 0)
W = (2 * pi / a, 2 * pi / a)
Y = (0, pi / a)
Z = (2 * pi / a, pi / a)
Q = (pi / a, 2 * pi / a)
RBME_points = [Gamma, X, M, Y]  # ,U, V, W, Z, Q]
N_RBME = 8
R = sim.get_rbme_matrix(N_RBME, RBME_points, polarization)

Nred = N_RBME * len(RBME_points)


eigenmodes_rbme = bk.empty((nk, nk, Nred, n_eig), dtype=bk.complex128)


for i in range(nk):
    _mode = []
    for j in range(nk):
        k = kx[i], ky[j]
        sim.k = k
        eigs, modes = sim.solve(polarization, rbme=R, reduced=True)
        eigenmodes_rbme[i, j] = modes[:, :n_eig]

for imode in range(n_eig):
    phi = sim.get_berry_curvature(
        kx, ky, eigenmodes_rbme[:, :, :, imode], method="rbme"
    )
    C = sim.get_chern_number(kx, ky, phi)
    print(f"Mode {imode+1}: Chern number = {C}")

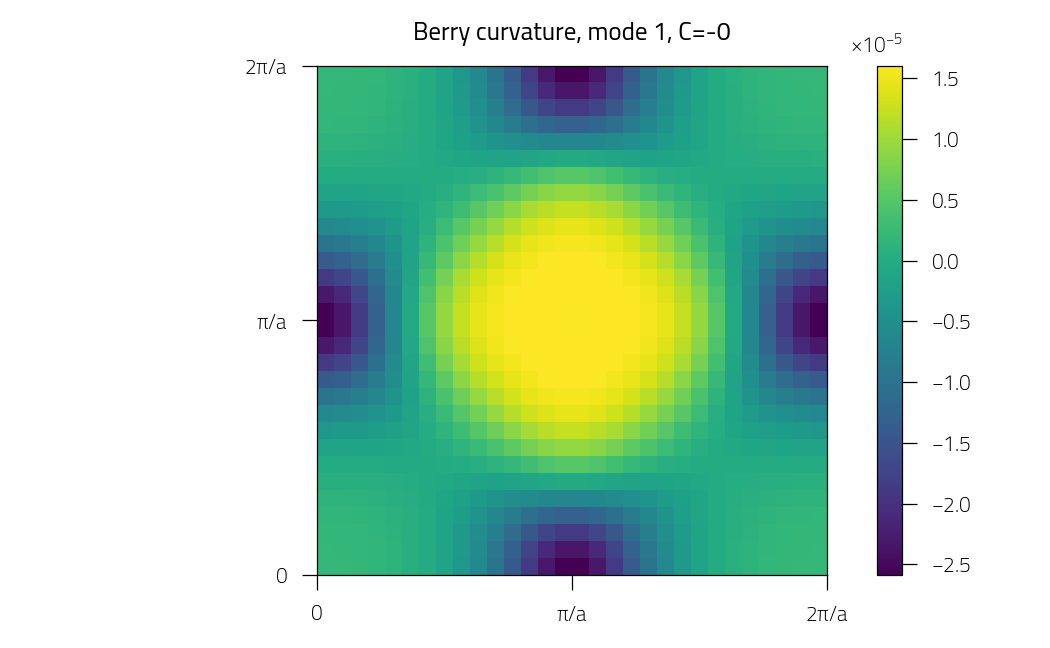
    plt.figure()
    plt.pcolormesh(kx, ky, phi)
    plt.axis("scaled")
    plt.xticks([0, pi / a, 2 * pi / a], ["0", r"$\pi/a$", r"$2\pi/a$"])
    plt.yticks([0, pi / a, 2 * pi / a], ["0", r"$\pi/a$", r"$2\pi/a$"])
    plt.title(f"Berry curvature, mode {imode+1}, C={C:.0f}")
    plt.colorbar()
    plt.tight_layout()
    plt.pause(0.001)


t += time.time()
print(f"Elapsed time RBME: {t:.1f}s")

• 
• 
• 

Mode 1: Chern number = -0.00025461078356810477
Mode 2: Chern number = -0.9989436451252299
Mode 3: Chern number = 1.9665374534479194
Elapsed time RBME: 26.3s

Estimated memory usage: 104 MB